Scanning Electron Microscopy
| PhenomXL SEM [SOP] | Phenom ProX SEM [SOP] | ||
|---|---|---|---|
| Magnification Range: | 160x to 200,000x | 80x to 130,000x | |
| Accelerating Voltages: | 4.8 kV to 20.5 kV (advanced mode) | 5, 10, or 15 kV | |
| Feature Resolution: | ~10nm | ~14nm | |
| Detectors: | Secondary (SED) & Backscatter (BSD) | Backscatter only | |
| Capabilities: | EDS, AIM, 3DRR | EDS | |
| Sample Dimensions: | max. 10 cm x 10 cm, 4 cm (h); or 36 stubs | max. 3.2 cm (ø), 3 cm (h) |
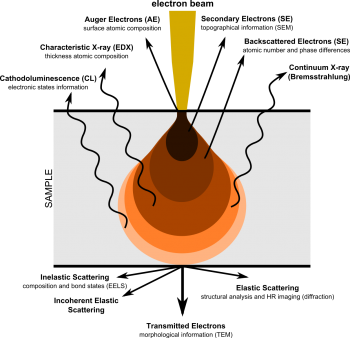
Scanning electron microscopy (SEM) rasters an electron beam across a specific area on a sample, allowing for much higher magnifications compared to optical microscopy. The electrons are either elastically or inelastically reflected off the sample, then captured by detector(s) to yield an image.
Electron Microscopy
Electron and optical microscopy share many fundamental components—specifically, a lens used to focus a specific type of source, and after either reflecting from or transmitting through the sample, a “signal” is then captured by a detector which processes inputs and spits out an image. In optical microscopy, an optical glass lens focuses photons from a lamp into either a digital camera or your eye. In electron microscopy, a series of variable magnetic fields serve as condenser lenses to vary the current and spot size of the electron beam (e-beam) generated from an electron gun. In SEM, this beam is then focused using an electromagnetic objective lens and rastered across the sample by a set of scan coils.
Similar to optical microscopy, electron microscopy also has both reflection and transmission modes—these are two separate imaging techniques known as Scanning Electron Microscopy (SEM) and Transmission Electron Microscopy (TEM), respectively.
Types of Electron Guns
There are 2 main types of electron guns used in electron microscopy: thermionic (Schottky) emission and cold field emission. Both types required an electron source—typically this is either a single crystal of tungsten, lanthanum hexaboride (LaB6), or cerium hexaboride (CeB6). Both Phenom SEMs at the MILL use thermionic emission guns with a CeB6 source.
Software Features
Automated Image Mapping (AIM): SEMs will raster beam over a larger area of a sample at a given magnification and automatically stitch the caputured images together.
3D Roughness Reconstruction (3DRR): SEM will attempt to focus in a range of depths, then stitch together planes of features which are in focus to generate a 3D image representative of surface topology. This can be exported as an image or .stl file.
Magnification & Resolution
SEMs can provide an additional 2 orders of magnitude in magnification and resolution when compared to optical microscopes, which typically max out around 1,000x magnification and 200 nm resolution. SEMs typically have around 100,000x magnification and 2 nm resolution. This additional resolution is governed by the Abbe equation and de Broglie wave equation.
Proof
Abbe’s equation defines the theoretical maximum resolution of a microscope, [math]\displaystyle{ \delta }[/math] as:
- [math]\displaystyle{ \delta=\frac{k\lambda}{n\sin(\alpha)} }[/math],
where [math]\displaystyle{ k = 0.61 }[/math] is an empirical constant, [math]\displaystyle{ n }[/math] is the refractive index, and [math]\displaystyle{ \alpha }[/math] is the aperture half-angle. The term in the denominator, [math]\displaystyle{ n\sin{\alpha)} }[/math], is also known as the numerical aperture, or nA.
In optical microscopy, Abbe’s equation simplifies to [math]\displaystyle{ \delta=\frac{0.61\lambda}{nA} }[/math], where the numerical aperture at high magnifications typically levels out at [math]\displaystyle{ nA \approx 1.35 }[/math]. Plugging in the [math]\displaystyle{ \lambda }[/math] for green light gives:
- [math]\displaystyle{ \delta=\frac{0.61\cdot500\textrm{nm}}{1.35}=226\textnormal{nm} }[/math]
In electron microscopy, the refractive index is typically 1, since the chamber is pumped down to near-vacuum conditions, and the aperture half-angle is typically very small. Using the small-angle approximation, we can simplify Abbe’s equation to
- [math]\displaystyle{ \delta=\frac{0.61\lambda}{\alpha} }[/math].
Since electron microscopy uses an electron beam to image the sample, [math]\displaystyle{ \lambda }[/math] is now the de Broglie wavelength of an electron. The de Broglie wave equation states:
- [math]\displaystyle{ \lambda=\frac{h}{p} }[/math],
where [math]\displaystyle{ h }[/math] is Planck’s constant and [math]\displaystyle{ p }[/math] is momentum. Recall that kinetic energy is defined as:
- [math]\displaystyle{ \textrm{KE} = \frac{1}{2}mv^2 }[/math]
- [math]\displaystyle{ \therefore p=mv=\sqrt{2m(\textrm{KE})} }[/math]
Electron microscopes such as SEMs typically have a controllable accelerating voltage—this term affects the kinetic energy of the e-beam by the fundamental relation: [math]\displaystyle{ \textrm{KE} = e\textrm{V} }[/math], where [math]\displaystyle{ e }[/math] is the elementary charge. Plugging in for momentum and kinetic energy, we get:
- [math]\displaystyle{ \therefore \lambda=\frac{h}{\sqrt{2me\textrm{V}}} }[/math]
Finally, by plugging in all constants and assuming a small aperture half-angle of 0.01 rad (must use radians for small-angle approximation), the following resolutions can be obtained for varying accelerating voltages. Note that these calculations use Newtonian equations, not Einsteinian (relativistic) equations.
| Accelerating Voltage (kV) | de Broglie Wavelength (nm) | Abbe Resolution (nm) |
|---|---|---|
| 5 | .0173 | 1.06 |
| 10 | .0123 | .751 |
| 15 | .0100 | .613 |
| 100 | .00388 pm | .237 |
Limitations
Despite the near-atomic resolution claimed by Abbe’s equation at higher accelerating voltages, SEMs struggle to reach beyond nanometer-level resolution, and therefore cannot see individual atoms. There are many variables which cause the reduction in practical resolution, so only major factors are listed here.
Interaction Volume
The first limitation is electron interaction volume. When a high energy electron beam strikes the sample, electrons penetrate the sample and knock free other electrons, ballooning into a relatively large interaction volume. The greater the accelerating voltage, the greater the interaction volume—therefore, SEMs must balance the improvement in theoretical Abbe resolution from a higher energy and the decrease in resolution from larger interaction volumes at high accelerating voltages.
Interaction volume typically has a diameter in the micron range for bulk samples and a diameter in the same order as sample thickness for thin foils used in TEM. This tiny interaction volume is also why extremely thin (<50nm) TEM foils can get down to atomic resolution. For SEM samples, noise and overlapping signals from different areas of a sample will blur an image if the accelerating voltage and interaction volume are too large. Ideally, interaction volume diameter should approximate the size of sample features to get sharp images.
Aberrations
Aberrations occur when a lens fails to converge all rays at a single point and the image becomes out of focus. There are two types of aberrations: spherical and chromatic. In SEM, spherical aberrations occur when electrons near the edges of an electromagnetic lens are bent inconsistently compared to electrons at the center of the lens and fail to converge—this can be fixed by using a smaller aperture. Chromatic aberrations occur when the electron beam is not of uniform energy, causing the electromagnetic lens to bend electrons of differing energies to different points on the focal plane. Both of these phenomena derive their names from the same photon-based effects in optical microscopy.
Astigmatism
Astigmatism in SEM occurs due to fluctuations in magnetic field strength, which may be caused by defects in the electron column core, source contamination, or magnetic samples. This typically results in the blurring or stretching of the SEM image, and can be corrected using stigmation coils. Most SEMs have both an X and Y stigmator knobs for correcting stretching, as well as an auto-stigmation feature.
Information Provided by SEM Emissions
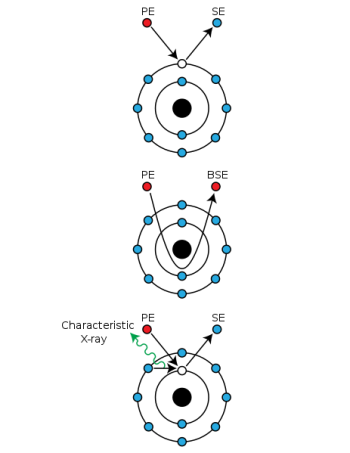
When primary electrons (PE) from the e-beam inelastically interact with electrons in the sample, they transfer a significant portion of their kinetic energy to another electron, which is then ejected as a secondary electron (SE). Other times, primary electrons can "slingshot" around atomic nuclei and return while only losing a negligible amount of energy. This is an elastic interaction, and the returned primary electrons are redubbed backscattered electrons (BSD). While SE have energies in the 10s of eVs, BSE return with the same initial energy, which varies based on accelerating voltage (10 kV accelerating voltage [math]\displaystyle{ \Rightarrow }[/math] 10 keV of energy). Therefore, SEMs primarily handle 2 detectors used for imaging: these are the secondary electron detector (SED) and the backscattered electron detector (BSD).
SED
Secondary electrons give an image which shows topographical features and a relatively large depth of field.
Since SEs have such low energies, they can only escape when present in the sample's surface (the top several nm). This also means SEs have low interaction volume, and have resolutions on the nm level. The most common type of SED is the Everhart-Thornley (ET) detector, which are placed off-center from the sample to provide better contrast between SEs coming from different areas on the sample surface in exchange for slightly worse signal-to-noise ratio. The reasoning for sacrificing signal is because SE yields (# of emitted SEs per PE) are over 100%—this is because high-energy PEs undergoing inelastic interactions can dislodge multiple SEs at a time.
BSD
Backscattered electrons give elemental contrast (Z-contrast), but by using a 4-quadrant detector, some topographical features are also resolvable. Turning off half of a 4-quadrant BSD works similarly to ET SEDs, where one side of sample will appear brighter than the other side. Note that these topographical modes do lose some Z-contrast in the process.
BSEs are very high energy, and therefore penetrate deeper into the sample than SEs. This larger interaction volume results in BSD resolutions in the 100s of nm, 2 orders of magnitude worse than SEDs. Additionally, BSE yields are typically under 50% because they cannot "share" their initial energy and some BSEs become trapped in atomic orbitals. Z-contrast occurs because of increasing nucleus size through the periodic table—heavier nuclei will more effectively "slingshot" PEs, result in greater counts for heavier atoms and lower counts for lighter atoms. This is typically displayed by making atomically heavier areas of the sample bright and atomically lighter areas of the sample dark.
EDS
Additionally, inelastic interactions which dislodge secondary electrons leave an electron vacancy which must be quenched, similar to X-ray fluorescence spectroscopy (XRF). The resulting vacancy is quenched, and the surplus energy is ejected as a secondary characteristic X-ray. Since energy drops between electrons levels in a given atom are discrete and distinct, a detector which can catch these secondary X-rays would be able to determine elemental composition. This is known as energy-dispersive X-ray spectroscopy (EDS/EDX), as is very common in SEM systems. Unlike XRF, secondary X-rays are only emitted from a small spot—more specifically, it is sensitive to interaction volume, which is typically 1-2 μm in diameter for characteristic X-rays, with a spot size of a few nm. For comparison XRF depth ranges from several μm to a few mm, and irradiates the entire sample at once. This makes EDS slightly more surface sensitive, while XRF is more bulk sensitive. In SEM, rastering the e-beam source across the sample generates an EDS map, which is useful to measue elemental composition of specific surface features such as pores and inclusions, as well as compositional differeneces across grain boundaries.
EBSD
Electron backscatter diffraction (EBSD) is a characterization technique found in some SEMs which gives detailed crystollographic information typically only available from techniques such as TEM or XRD. EBSD requires a crystalline sample polished to a flat surface to improve the signal-to-noise ratio of diffraction bands and lattice quality. The sample must also be highly tilted (~70º from horizontal) with respect to the diffraction camera (placed perpendicular to the e-beam) to increase diffraction contrast for the camera's phosphor screen, and the sample must be placed extremely close to the camera to increase signal (low working distance, WD < 5mm for most SEMs). The backscattered electrons which escape at this specific angle must follow the Bragg diffraction condition, resulting signal bands seen on the camera known as Kikuchi lines or Kikuchi bands.
Depth of Field
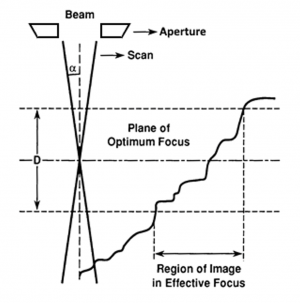
Electron microscopy, specifically when detecting secondary electrons, has a superior depth of field compared to optical microscopy. Depth of field is a objective measure of the ability of a microscope to simultaneously focus at multiple depth—more specifically, it is the "acceptable range" of depths where sample features are still in focus. Mathematically, depth of field, [math]\displaystyle{ D }[/math], can be approximated by:
- [math]\displaystyle{ D=\frac{2r}{\tan{\alpha}} }[/math],
where [math]\displaystyle{ r }[/math] is the radius of the viewing spot, and [math]\displaystyle{ \alpha }[/math] is again the aperture half-angle. This formula can be confirmed upon inspection of the diagram to the right. This small aperture half-angle is what gives SEMs a much better depth of field that optical microscopes, whose aperture half angles are much larger. For SEMs, we can once again use the small-angle approximation to simplify this to:
- [math]\displaystyle{ D=\frac{2r}{\alpha} }[/math]
Since depth of field is subjective and based on the image itself, note that this viewing spot is actually the defined by the area on the sample which corresponds to a single pixel of the image. This area can therefore be calculated using the SEM's field of view, [math]\displaystyle{ W_\textrm{FOV} }[/math], and the pixel width of the image, [math]\displaystyle{ W_\textrm{pix} }[/math]:
- [math]\displaystyle{ 2r=\frac{W_\textrm{FOV}}{W_\textrm{pix}} }[/math]
Alternatively, if given the image's actual pixel size (a constant diameter), [math]\displaystyle{ P }[/math], we can define magnification, [math]\displaystyle{ M }[/math], to be:
- [math]\displaystyle{ M=\frac{P}{2r} \rightarrow 2r=\frac{P}{M} }[/math]
This shows that the size of the viewing spot depends on image magnification: therefore, magnification also affects the depth of field.
- [math]\displaystyle{ \therefore D=\frac{P}{M\alpha} }[/math]
From this equation, we can see that lowering either the aperture half-angle or the magnification will result in a greater depth of field in SEMs.
Working Distance
Since magnification cannot be changed if we want to continue to view small features, the aperture can be tweaked through the working distance, or WD. WD is the distance between the bottom pole piece of the objective lens and the specimen. Given the objective aperture radius [math]\displaystyle{ R }[/math], [math]\displaystyle{ \alpha }[/math] can be defined as:
- [math]\displaystyle{ \alpha=\frac{R}{\textrm{WD}} }[/math]
WD typically falls between 5-9 mm when using secondary electron detectors.
Common SEM Issues
SEMs run into several unavoidable issues which requires users to prepare and analyze samples more carefully.
Sample Charging
Since SEMs blast a sample with electrons, samples will always charge wil imaging. The polarity of charge depends on the sample, but typically the sample emits more electrons than the number of incident primary electrons due to a SE yield of over 100%. Therefore, the sample becomes slightly positively charged. A charged sample results in several complications for SEM, whether positively or negatively charged. Charged samples will deflect both the primary e-beam at the surface and the emitted electrons. This disturbs focus, depth of field, and contrast, distorts and drifts the image, creates random dark and bright spots/streaks on the image, and in extreme cases, charging can even break parts of the specimen and damage the detector and source.
To avoid this, several precautions can be taken during sample prep and during analysis. Firstly, either carbon or copper tape should be used to afix the sample to the sample stub or holder so that the sample is grounded. This allows electrons to freely travel to fill electron-holes in the sample to maintain a neutral charge. Non-conductive samples should be coated with gold nanoparticles (see Sputter Coater) to make the sample conductive—this allows topographical features to still be visible, although it will dampen contrast in BSD images and muddle EDS with gold peaks. If BSD or EDS are wanted, the sample should instead be imaged at a low accelerating voltage on the SEM (5kV) and rastering speed should be increased to avoid significant charging at any one spot. Conductive samples simply need to be grounded to the sample stub or holder. For samples mounted in a hot mounting press, use a conductive mounting compound (such as conductive phenolic powders) or afix carbon or copper tape directly onto the sample surface and ground point.
Sample Etching
When a higher energy e-beam rasters across one region for a prolonged duration, it may "etch" the sample by depositing a thin layer of residue. This residue comes from gases which were not pumped out by the vacuum, namely, hydrocarbons and water. High energy electrons can help water and carbon "stick" ot the sample, and upon increasing your field of view in the imaging software, a darkened box may be visible on your sample—this is a sign of etching. This phenomena is especially prevalent at higher magnifications, where the beam continually rasters over an even smaller spot. This is unpreventable, but during analysis, it is recommended to not stay in one place for a long time and to keep moving around. When examining small features that require high magnification, focus on another small feature in the same plane as your feature, then move to your area of interest to avoid etching imporant areas.
"Dangerous" Samples
Any sample with loose particles may break under an intense e-beam and damage the detector and source—samples must be firmly attached to the sample stub or holder. Because lenses in electron microscopes are controlled using precise electromagnetic fields, magnetic samples may permamently damage the objective lens and are therefore not allowed in many SEMs. Porous samples suck as rock and concrete may contain trapped gases which may degas if put under high vacuum in the SEM. These gases may damage the detector and source, so samples should be degassed (and dried) before analysis.